2.7. Plotting Kwant systems and data in various styles

The plotting functionality of Kwant has been used extensively (through plot and map) in the previous tutorials. In addition to this basic use, plot offers many options to change the plotting style extensively. It is the goal of this tutorial to show how these options can be used to achieve various very different objectives.

2.7.1. 2D example: graphene quantum dot

See also

The complete source code of this example can be found in tutorial/plot_graphene.py

We begin by first considering a circular graphene quantum dot (similar to what has been used in parts of the tutorial Beyond square lattices: graphene.) In contrast to previous examples, we will also use hoppings beyond next-nearest neighbors:

lat = kwant.lattice.honeycomb()
a, b = lat.sublattices

def make_system(r=8, t=-1, tp=-0.1):

    def circle(pos):
        x, y = pos
        return x**2 + y**2 < r**2

    sys = kwant.Builder()
    sys[lat.shape(circle, (0, 0))] = 0
    sys[lat.neighbors()] = t
    sys.eradicate_dangling()
    if tp:
        sys[lat.neighbors(2)] = tp

    return sys

Note that adding hoppings hoppings to the n-th nearest neighbors can be simply done by passing n as an argument to neighbors. Also note that we use the method eradicate_dangling to get rid of single atoms sticking out of the shape. It is necessary to do so before adding the next-nearest-neighbor hopping [1].

Of course, the system can be plotted simply with default settings:

def plot_system(sys):
    kwant.plot(sys)

However, due to the richer structure of the lattice, this results in a rather busy plot:

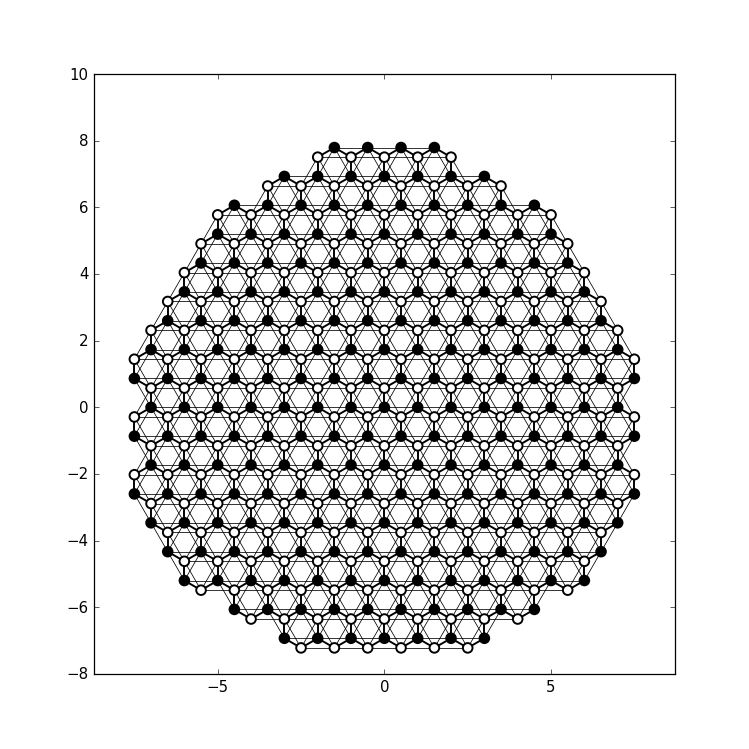
A much clearer plot can be obtained by using different colors for both sublattices, and by having different line widths for different hoppings. This can be achieved by passing a function to the arguments of plot, instead of a constant. For properties of sites, this must be a function taking one site as argument, for hoppings a function taking the start end end site of hopping as arguments:

    def family_color(site):
        return 'black' if site.family == a else 'white'

    def hopping_lw(site1, site2):
        return 0.04 if site1.family == site2.family else 0.1

    kwant.plot(sys, site_lw=0.1, site_color=family_color, hop_lw=hopping_lw)

Note that since we are using an unfinalized Builder, a site is really an instance of Site. With these adjustments we arrive at a plot that carries the same information, but is much easier to interpret:

Apart from plotting the system itself, plot can also be used to plot data living on the system.

As an example, we now compute the eigenstates of the graphene quantum dot and intend to plot the wave function probability in the quantum dot. For aesthetic reasons (the wave functions look a bit nicer), we restrict ourselves to nearest-neighbor hopping. Computing the wave functions is done in the usual way (note that for a large-scale system, one would probably want to use sparse linear algebra):

def plot_data(sys, n):
    import scipy.linalg as la

    sys = sys.finalized()
    ham = sys.hamiltonian_submatrix()
    evecs = la.eigh(ham)[1]

    wf = abs(evecs[:, n])**2

In most cases, to plot the wave function probability, one wouldn’t use plot, but rather map. Here, we plot the n-th wave function using it:

    kwant.plotter.map(sys, wf, oversampling=10, cmap='gist_heat_r')

This results in a standard pseudocolor plot, showing in this case (n=225) a graphene edge state, i.e. a wave function mostly localized at the zigzag edges of the quantum dot.

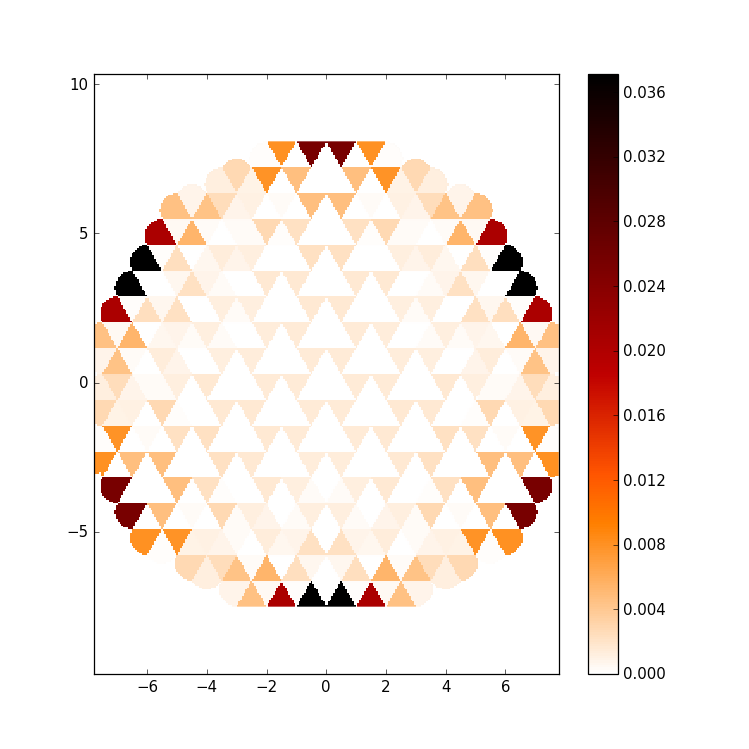
However although in general preferable, map has a few deficiencies for this small system: For example, there are a few distortions at the edge of the dot. (This cannot be avoided in the type of interpolation used in map). However, we can also use plot to achieve a similar, but smoother result.

For this note that plot can also take an array of floats (or function returning floats) as value for the site_color argument (the same holds for the hoppings). Via the colormap specified in cmap these are mapped to color, just as map does! In addition, we can also change the symbol shape depending on the sublattice. With a triangle pointing up and down on the respective sublattice, the symbols used by plot fill the space completely:

    def family_shape(i):
        site = sys.site(i)
        return ('p', 3, 180) if site.family == a else ('p', 3, 0)

    def family_color(i):
        return 'black' if sys.site(i).family == a else 'white'

    kwant.plot(sys, site_color=wf, site_symbol=family_shape,
               site_size=0.5, hop_lw=0, cmap='gist_heat_r')

Note that with hop_lw=0 we deactivate plotting the hoppings (that would not serve any purpose here). Moreover, site_size=0.5 guarantees that the two different types of triangles touch precisely: By default, plot takes all sizes in units of the nearest-neighbor spacing. site_size=0.5 thus means half the distance between neighboring sites (and for the triangles this is interpreted as the radius of the inner circle).

Finally, note that since we are dealing with a finalized system now, a site i is represented by an integer. In order to obtain the original Site, sys.site(i) can be used.

With this we arrive at

with the same information as map, but with a cleaner look.

The way how data is presented of course influences what features of the data are best visible in a given plot. With plot one can easily go beyond pseudocolor-like plots. For example, we can represent the wave function probability using the symbols itself:

    def site_size(i):
        return 3 * wf[i] / wf.max()

    kwant.plot(sys, site_size=site_size, site_color=(0, 0, 1, 0.3),
               hop_lw=0.1)

Here, we choose the symbol size proportional to the wave function probability, while the site color is transparent to also allow for overlapping symbols to be visible. The hoppings are also plotted in order to show the underlying lattice.

With this, we arrive at

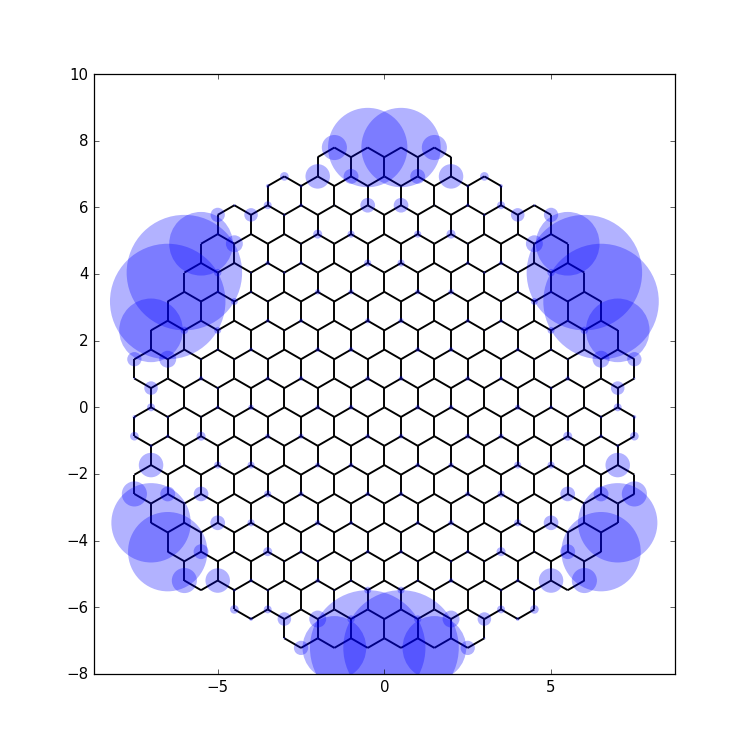
which shows the edge state nature of the wave function most clearly.

Footnotes

[1]	A dangling site is defined as having only one hopping connecting it to the rest. With next-nearest-neighbor hopping also all sites that are dangling with only nearest-neighbor hopping have more than one hopping.

2.7.2. 3D example: zincblende structure

See also

The complete source code of this example can be found in tutorial/plot_zincblende.py

Zincblende is a very common crystal structure of semiconductors. It is a face-centered cubic crystal with two inequivalent atoms in the unit cell (i.e. two different types of atoms, unlike diamond which has the same crystal structure, but two equivalent atoms per unit cell).

It is very easily generated in Kwant with kwant.lattice.general:

lat = kwant.lattice.general([(0, 0.5, 0.5), (0.5, 0, 0.5), (0.5, 0.5, 0)],
                            [(0, 0, 0), (0.25, 0.25, 0.25)])
a, b = lat.sublattices

Note how we keep references to the two different sublattices for later use.

A three-dimensional structure is created as easily as in two dimensions, by using the shape-functionality:

def make_cuboid(a=15, b=10, c=5):
    def cuboid_shape(pos):
        x, y, z = pos
        return 0 <= x < a and 0 <= y < b and 0 <= z < c

    sys = kwant.Builder()
    sys[lat.shape(cuboid_shape, (0, 0, 0))] = None
    sys[lat.neighbors()] = None

    return sys

We restrict ourselves here to a simple cuboid, and do not bother to add real values for onsite and hopping energies, but only the placeholder None (in a real calculation, several atomic orbitals would have to be considered).

plot can plot 3D systems just as easily as its two-dimensional counterparts:

    sys = make_cuboid()

    kwant.plot(sys)

resulting in

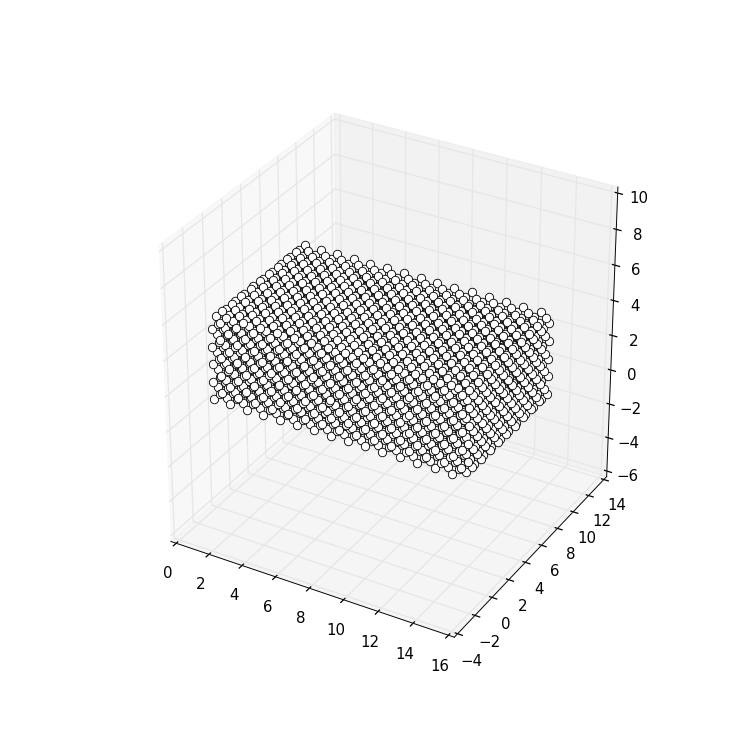
You might notice that the standard options for plotting are quite different in 3D than in 2D. For example, by default hoppings are not printed, but sites are instead represented by little “balls” touching each other (which is achieved by a default site_size=0.5). In fact, this style of plotting 3D shows quite decently the overall geometry of the system.

When plotting into a window, the 3D plots can also be rotated and scaled arbitrarily, allowing for a good inspection of the geometry from all sides.

Note

Interactive 3D plots usually do not have the proper aspect ratio, but are a bit squashed. This is due to bugs in matplotlib’s 3D plotting module that does not properly honor the corresponding arguments. By resizing the plot window however one can manually adjust the aspect ratio.

Also for 3D it is possible to customize the plot. For example, we can explicitly plot the hoppings as lines, and color sites differently depending on the sublattice:

    sys = make_cuboid(a=1.5, b=1.5, c=1.5)

    def family_colors(site):
        return 'r' if site.family == a else 'g'

    kwant.plot(sys, site_size=0.18, site_lw=0.01, hop_lw=0.05,
               site_color=family_colors)

which results in a 3D plot that allows to interactively (when plotted in a window) explore the crystal structure:

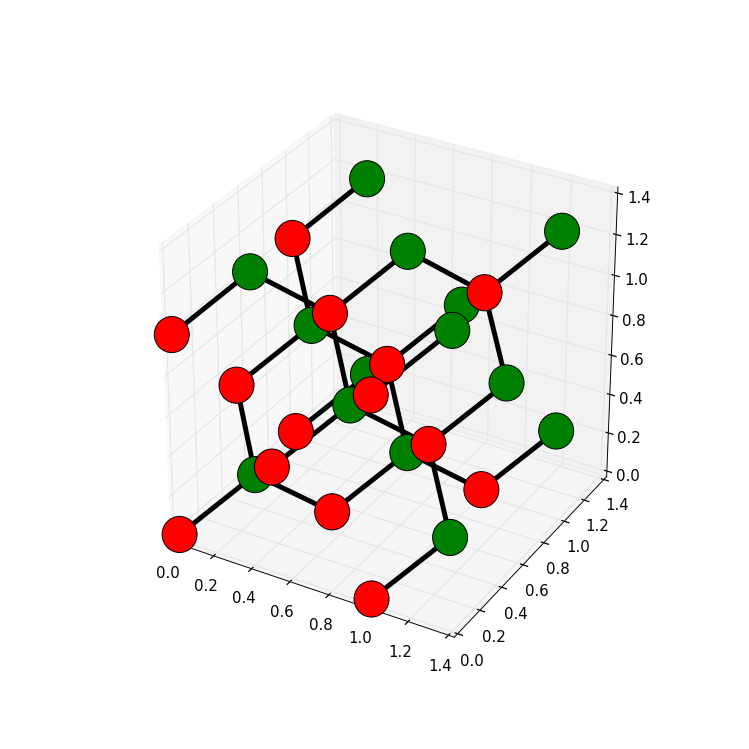
Hence, a few lines of code using Kwant allow to explore all the different crystal lattices out there!

Note

• The 3D plots are in fact only fake 3D. For example, sites will always be plotted above hoppings (this is due to the limitations of matplotlib’s 3d module)
• Plotting hoppings in 3D is inherently much slower than plotting sites. Hence, this is not done by default.