This article explains the user-visible changes in Kwant 1.3.0, released on 19 May 2017. See also the full list of changes up to the most recent bugfix release of the 1.3 series.
Builders now have a fill method that fills a builder
instance with copies of a template builder. This can be used to “cut out”
shapes from high-symmetry models, or to increase the symmetry period of a lead.
Thus Kwant gains the new concept of a “model”. Models may be created manually,
or with the new function kwant.continuum.discretize (see next paragraph).
There is also support for finalizing models and e.g. calculating their band
structure (see Finalizing builders with multiple translational symmetries).
The new sub-package continuum is a collection of tools for working
with continuum models and for discretizing them into tight-binding models. It
aims at providing a handy interface to convert symbolic Hamiltonians into a
builder with N-D translational symmetry that can be use to calculate
tight-binding band structures or construct systems with different/lower
symmetry. For example in just a few lines we can construct a two-band model that exhibits
a quantum anomalous spin Hall phase:
def make_model(a):
ham = ("alpha * (k_x * sigma_x - k_y * sigma_y)"
"+ (m + beta * kk) * sigma_z"
"+ (gamma * kk + U) * sigma_0")
subs = {"kk": "k_x**2 + k_y**2"}
return kwant.continuum.discretize(ham, locals=subs, grid=a)
From: QAHE example script
See the tutorial: Discretizing continuous Hamiltonians
See the reference documentation: kwant.continuum – Tools for continuum systems
Often one may wish to calculate quantities that are defined over sites of
the system (such as charge density, spin density along some axis etc),
or over hoppings of the system (such as current or spin current). With
the introduction of the operator module it has now become much easier
to calculate such quantities. To obtain the regular density and current
everywhere in a system due to a wavefunction psi, one only needs to do
the following:
syst = make_system().finalized()
psi = kwant.wave_function(syst)(0)[0]
# create the operators
Q = kwant.operator.Density(syst)
J = kwant.operator.Current(syst)
# evaluate the expectation value with the wavefunction
q = Q(psi)
j = J(psi)
See the tutorial: Computing local quantities: densities and currents
Quantities defined on system hoppings (e.g. currents calculated using
Current) can be directly plotted as a streamplot over the
system using kwant.plotter.current. This is similar to how
kwant.plotter.map can be used to plot quantities defined on sites.
The example below shows edge states of a quantum anomalous Hall phase
of the two-band model shown in the above section:
J = kwant.operator.Current(syst).bind(params=params)
current = sum(J(p) for p in psi)
kwant.plotter.current(syst, current)
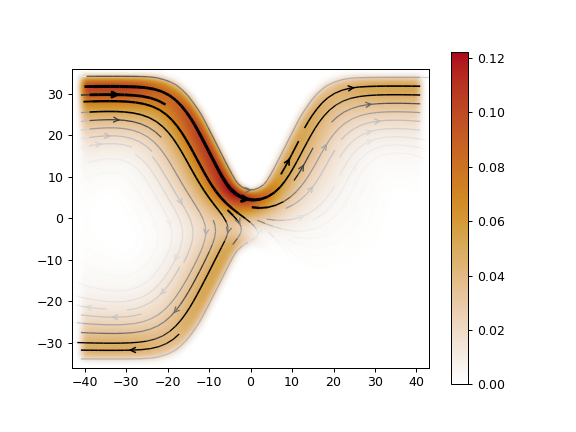
From: QAHE example script
Given a lead Hamiltonian that has a conservation law, it is now possible to construct lead modes that have definite values of the conservation law. This is done by declaring projectors that block diagonalize the Hamiltonian before the modes are computed. For a Hamiltonian that has one or more of the three fundamental discrete symmetries (time-reversal symmetry, particle-hole symmetry and chiral symmetry), it is now possible to declare the symmetries in Kwant. The symmetries are then used to construct scattering states that are properly related by symmetry. The discrete symmetries may be combined with conservation laws, such that if different blocks of the Hamiltonian are related by a discrete symmetry, the lead modes are computed to reflect this.
See the updated tutorial: Superconductors: orbital degrees of freedom, conservation laws and symmetries
In Kwant < 1.3 whenever Hamiltonian values were provided as functions, they all had to take the same extra parameters (after the site(s)) regardless of whether or not they actually used them at all. For example, if we had some onsite potential and a magnetic field that we model using the Peierls substitution, we would have to define our value functions like so:
# formally depends on 'B', but 'B' is never used
def onsite(site, V, B):
return V
# formally depends on 'V', but 'V' is never used
def hopping(site_a, site_b, V, B):
return (site_b.pos[1] - site_a.pos[1]) * B
This was because previously extra arguments were provided to the system
by passing them as a sequence via the args parameter to various Kwant
functions (e.g. kwant.smatrix or hamiltonian_submatrix).
In Kwant 1.3 it is now possible for value functions to depend on different parameters, e.g.:
def onsite(site, V):
return V
def hopping(site_a, site_b, B):
return (site_b.pos[1] - site_a.pos[1]) * B
If you make use of this feature then you must in addition pass your arguments
via the params parameter. The value provided to params must
be a dict that maps parameter names to values, e.g.:
kwant.smatrix(syst, params=dict(B=0.1, V=2))
as opposed to the old way:
kwant.smatrix(syst, args=(2, 0.1))
Passing a dictionary of parameters via params is now the recommended way
to provide parameters to the system.
The kernel polynomial method is now implemented within Kwant to obtain the density of states or, more generally, the spectral density of a given operator acting on a system or Hamiltonian.
See the tutorial: Calculating spectral density with the kernel polynomial method
See the reference documentation: kwant.kpm – Kernel Polynomial Method
While it remains impossible to finalize a builder with more than a single
direction of translational symmetry, the wraparound module has been added
as a temporary work-around until the above limitation gets lifted.
The function wraparound transforms all (or all but one)
translational symmetries of a given builder into named momentum parameters
k_x, k_y, etc. This makes it easy to compute transport through systems
with periodic boundary conditions or across infinite planes.
Plotting the 2-d band structure of graphene is now as straightforward as:
from matplotlib import pyplot
import kwant
lat = kwant.lattice.honeycomb()
sym = kwant.TranslationalSymmetry(lat.vec((1, 0)), lat.vec((0, 1)))
bulk = kwant.Builder(sym)
bulk[ [lat.a(0, 0), lat.b(0, 0)] ] = 0
bulk[lat.neighbors()] = 1
wrapped = kwant.wraparound.wraparound(bulk).finalized()
kwant.wraparound.plot_2d_bands(wrapped)
In Python 3 the internal ordering of dictionaries is not deterministic. This meant that running a Kwant script twice would produce systems with different ordering of sites, which leads to non-reproducible calculations. Now, sites in finalized builders are always ordered first by their site family, then by their tag.
Coincidentally, this means that you can plot a wavefunction in a simple 1D system by just saying:
lattice_1D = chain()
syst = make_system(lattice_1D)
h = syst.hamiltonian_submatrix()
pyplot.plot(np.eigs(h)[1][0])
When attaching a lead with greater than nearest-neighbor hoppings, the symmetry period of the finalized lead is suitably extended and the unit cell size is increased.
The name of the build configuration file, build.conf by default, is now
configurable with the --configfile=PATH option to setup.py. (This
makes build configuration usable with the pip tool.) The build
configuration as specified in this file is now more general, allowing to
modify any build parameter for any of the compiled extensions contained in
Kwant. See the Installation instructions for
details.
Given a site, the method neighbors of
Builder returns an iterator over sites that are connected by a
hopping to the provided site. This is in contrast to previous versions of
Kwant, where the neighbors were yielded not of the provided site, but of it’s
image in the fundamental domain.
This change is documented here for completeness. We expect that the vast majority of users of Kwant will not be affected by it.
The hamiltonian method of low-level systems must now accept a
params keyword parameter.