As first example, we compute the transmission probability through a two-dimensional quantum wire. The wire is described by the two-dimensional Schrödinger equation

with a hard-wall confinement 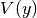 in y-direction.
in y-direction.
To be able to implement the quantum wire with Kwant, the continuous Hamiltonian
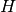 has to be discretized thus turning it into a tight-binding
model. For simplicity, we discretize
has to be discretized thus turning it into a tight-binding
model. For simplicity, we discretize 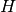 on the sites of a square
lattice with lattice constant
on the sites of a square
lattice with lattice constant  . Each site with the integer
lattice coordinates
. Each site with the integer
lattice coordinates 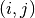 has the real-space coordinates
has the real-space coordinates 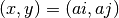 .
.
Introducing the discretized positional states
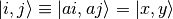
the second-order differential operators can be expressed in the limit 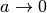 as
as
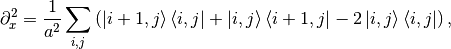
and an equivalent expression for 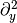 . Subsitituting them in
the Hamiltonian gives us
. Subsitituting them in
the Hamiltonian gives us
![H = \sum_{i,j} \big[ \left(V(ai, aj) + 4t\right)\ket{i,j}\bra{i,j}
- t \big( \ket{i+1,j}\bra{i,j} + \ket{i,j}\bra{i+1,j}
+ \ket{i,j+1}\bra{i,j} + \ket{i,j}\bra{i,j+1} \big) \big]](../_images/math/475e4688a6426efeb1c93fe542240326736b1a37.png)
with
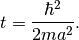
For finite  , this discretized Hamiltonian approximates the continuous
one to any required accuracy. The approximation is good for all quantum states
with a wave length considerably larger than
, this discretized Hamiltonian approximates the continuous
one to any required accuracy. The approximation is good for all quantum states
with a wave length considerably larger than  .
.
The remainder of this section demonstrates how to realize the discretized
Hamiltonian in Kwant and how to perform transmission calculations. For
simplicity, we choose to work in such units that  .
.
See also
The complete source code of this example can be found in
tutorial/quantum_wire.py
In order to use Kwant, we need to import it:
import kwant
Enabling Kwant is as easy as this [1] !
The first step is now the definition of the system with scattering region and
leads. For this we make use of the Builder type that allows to
define a system in a convenient way. We need to create an instance of it:
sys = kwant.Builder()
Observe that we just accessed Builder by the name
kwant.Builder. We could have just as well written
kwant.builder.Builder instead. Kwant consists of a number of sub-packages
that are all covered in the reference documentation. For convenience, some of the most widely-used members
of the sub-packages are also accessible directly through the top-level kwant
package.
Apart from Builder we also need to specify
what kind of sites we want to add to the system. Here we work with
a square lattice. For simplicity, we set the lattice constant to unity:
a = 1
lat = kwant.lattice.square(a)
Since we work with a square lattice, we label the points with two
integer coordinates (i, j). Builder then
allows us to add matrix elements corresponding to lattice points:
sys[lat(i, j)] = ... sets the on-site energy for the point (i, j),
and sys[lat(i1, j1), lat(i2, j2)] = ... the hopping matrix element
from point (i2, j2) to point (i1, j1).
Note that we need to specify sites for Builder
in the form lat(i, j). The lattice object lat does the
translation from integer coordinates to proper site format
needed in Builder (more about that in the technical details below).
We now build a rectangular scattering region that is W lattice points wide and L lattice points long:
t = 1.0
W = 10
L = 30
# Define the scattering region
for i in xrange(L):
for j in xrange(W):
# On-site Hamiltonian
sys[lat(i, j)] = 4 * t
# Hopping in y-direction
if j > 0:
sys[lat(i, j), lat(i, j - 1)] = -t
# Hopping in x-direction
if i > 0:
sys[lat(i, j), lat(i - 1, j)] = -t
Observe how the above code corresponds directly to the terms of the discretized Hamiltonian: “On-site Hamiltonian” implements
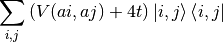
(with zero potential). “Hopping in x-direction” implements
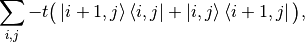
and “Hopping in y-direction” implements
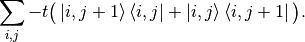
The hard-wall confinement is realized by not having hoppings (and sites) beyond a certain region of space.
Next, we define the leads. Leads are also constructed using
Builder, but in this case, the
system must have a translational symmetry:
sym_left_lead = kwant.TranslationalSymmetry((-a, 0))
left_lead = kwant.Builder(sym_left_lead)
Here, the Builder takes a
TranslationalSymmetry as the optional parameter. Note that the
(real-space) vector (-a, 0) defining the translational symmetry must point
in a direction away from the scattering region, into the lead – hence, lead
0 [2] will be the left lead, extending to infinity to the left.
For the lead itself it is enough to add the points of one unit cell as well as the hoppings inside one unit cell and to the next unit cell of the lead. For a square lattice, and a lead in y-direction the unit cell is simply a vertical line of points:
for j in xrange(W):
left_lead[lat(0, j)] = 4 * t
if j > 0:
left_lead[lat(0, j), lat(0, j - 1)] = -t
left_lead[lat(1, j), lat(0, j)] = -t
Note that here it doesn’t matter if you add the hoppings to the next or the previous unit cell – the translational symmetry takes care of that. The isolated, infinite is attached at the correct position using
sys.attach_lead(left_lead)
This call returns the lead number which will be used to refer to the lead when computing transmissions (further down in this tutorial). More details about attaching leads can be found in the tutorial Nontrivial shapes.
We also want to add a lead on the right side. The only difference to the left lead is that the vector of the translational symmetry must point to the right, the remaining code is the same:
sym_right_lead = kwant.TranslationalSymmetry((a, 0))
right_lead = kwant.Builder(sym_right_lead)
for j in xrange(W):
right_lead[lat(0, j)] = 4 * t
if j > 0:
right_lead[lat(0, j), lat(0, j - 1)] = -t
right_lead[lat(1, j), lat(0, j)] = -t
sys.attach_lead(right_lead)
Note that here we added points with x-coordinate 0, just as for the left lead. You might object that the right lead should be placed L (or L+1?) points to the right with respect to the left lead. In fact, you do not need to worry about that.
Now we have finished building our system! We plot it, to make sure we didn’t make any mistakes:
kwant.plot(sys)
This should bring up this picture:

The system is represented in the usual way for tight-binding systems: dots represent the lattice points (i, j), and for every nonzero hopping element between points there is a line connecting these points. From the leads, only a few (default 2) unit cells are shown, with fading color.
In order to use our system for a transport calculation, we need to finalize it
sys = sys.finalized()
Having successfully created a system, we now can immediately start to compute its conductance as a function of energy:
energies = []
data = []
for ie in xrange(100):
energy = ie * 0.01
# compute the scattering matrix at a given energy
smatrix = kwant.smatrix(sys, energy)
# compute the transmission probability from lead 0 to
# lead 1
energies.append(energy)
data.append(smatrix.transmission(1, 0))
We use kwant.smatrix which is a short name for
kwant.solvers.default.smatrix of the default solver module
kwant.solvers.default. kwant.smatrix computes the scattering matrix
smatrix solving a sparse linear system. smatrix itself allows to
directly compute the total transmission probability from lead 0 to lead 1 as
smatrix.transmission(1, 0). The numbering used to refer to the leads here
is the same as the numbering assigned by the call to
attach_lead earlier in the tutorial.
Finally we can use matplotlib to make a plot of the computed data
(although writing to file and using an external viewer such as
gnuplot or xmgrace is just as viable)
pyplot.figure()
pyplot.plot(energies, data)
pyplot.xlabel("energy [t]")
pyplot.ylabel("conductance [e^2/h]")
pyplot.show()
This should yield the result
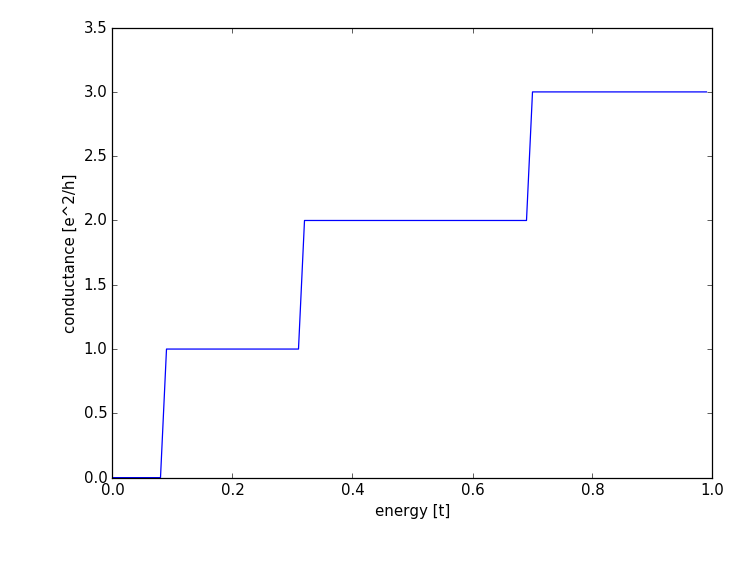
We see a conductance quantized in units of 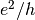 ,
increasing in steps as the energy is increased. The
value of the conductance is determined by the number of occupied
subbands that increases with energy.
,
increasing in steps as the energy is increased. The
value of the conductance is determined by the number of occupied
subbands that increases with energy.
In the example above, when building the system, only one direction
of hopping is given, i.e. sys[lat(i, j), lat(i, j-1)] = ... and
not also sys[lat(i, j-1), lat(i, j)] = .... The reason is that
Builder automatically adds the other
direction of the hopping such that the resulting system is Hermitian.
However, it does not hurt to define the opposite direction of hopping as well:
sys[lat(1, 0), lat(0, 0)] = -t
sys[lat(0, 0), lat(1, 0)] = -t.conj()
(assuming that t is complex) is perfectly fine. However, be aware that also
sys[lat(1, 0), lat(0, 0)] = -1
sys[lat(0, 0), lat(1, 0)] = -2
is valid code. In the latter case, the hopping sys[lat(1, 0),
lat(0, 0)] is overwritten by the last line and also equals to -2.
Some more details the relation between Builder
and the square lattice lat in the example:
Technically, Builder expects
sites as indices. Sites themselves have a certain type, and
belong to a site family. A site family is also used to convert
something that represents a site (like a tuple) into a
proper Site object that can be used with
Builder.
In the above example, lat is the site family. lat(i, j)
then translates the description of a lattice site in terms of two
integer indices (which is the natural way to do here) into
a proper Site object.
The concept of site families and sites allows Builder
to mix arbitrary lattices and site families
In the example, we wrote
sys = sys.finalized()
In doing so, we transform the Builder object (with which
we built up the system step by step) into a System
that has a fixed structure (which we cannot change any more).
Note that this means that we cannot access the Builder
object any more. This is not necesarry any more, as the computational
routines all expect finalized systems. It even has the advantage
that python is now free to release the memory occupied by the
Builder which, for large systems, can be considerable.
Roughly speaking, the above code corresponds to
fsys = sys.finalized()
del sys
sys = fsys
Even though the vector passed to the
TranslationalSymmetry is specified in real space, it must
be compatible with the lattice symmetries. A single lead can consists of
sites belonging to more than one lattice, but of course the translational
symmetry of the lead has to be shared by all of them.
Instead of plotting to the screen (which is standard)
plot can also write to a file specified by the argument
file. For the plotting to the screen to work the module
matplotlib.pyplot has to be imported. (An informative error message
will remind you if you forget.) The reason for this is pretty technical:
matplotlib’s “backend” can only be chosen before matplotlib.pyplot has
been imported. Would Kwant import that module by itself, it would deprive
you of the possibility to choose a non-default backend later.
Footnotes
| [1] | http://xkcd.com/353/ |
| [2] | Leads are numbered in the python convention, starting from 0. |
See also
The complete source code of this example can be found in
tutorial/quantum_wire_revisited.py
Kwant allows for more than one way to build a system. The reason is that
Builder is essentially just a container that can be filled in
different ways. Here we present a more compact rewrite of the previous example
(still with the same results).
Also, the previous example was written in the form of a Python script with little structure, and with everything governed by global variables. This is OK for such a simple example, but for larger projects it makes sense to partition the code into separate entities. In this example we therefore also aim at more structure.
We begin the program collecting all imports in the beginning of the file and put the build-up of the system into a separate function make_system:
import kwant
# For plotting
from matplotlib import pyplot
def make_system(a=1, t=1.0, W=10, L=30):
# Start with an empty tight-binding system and a single square lattice.
# `a` is the lattice constant (by default set to 1 for simplicity.
lat = kwant.lattice.square(a)
sys = kwant.Builder()
Previously, the scattering region was build using two for-loops.
Instead, we now write:
sys[(lat(x, y) for x in range(L) for y in range(W))] = 4 * t
Here, all lattice points are added at once in the first line. The
construct ((i, j) for i in xrange(L) for j in xrange(W)) is a
generator that iterates over all points in the rectangle as did the
two for-loops in the previous example. In fact, a
Builder can not only be indexed by a single
lattice point – it also allows for lists of points, or, as in this
example, a generator (as is also used in list comprehensions in
python).
Having added all lattice points in one line, we now turn to the hoppings. In this case, an iterable like for the lattice points becomes a bit cumbersome, and we use instead another feature of Kwant:
sys[lat.neighbors()] = -t
In regular lattices, hoppings form large groups such that hoppings within a
group can be transformed into one another by lattice translations. In order to
allow to easily manipulate such hoppings, an object
HoppingKind is provided. When given a Builder
as an argument, HoppingKind yields all the hoppings of a
certain kind that can be added to this builder without adding new sites. When
HoppingKind is given to Builder as a key, it
means that something is done to all the possible hoppings of this kind. A list
of HoppingKind objects corresponding to nearest neighbors in
lattices in Kwant is obtained using lat.neighbors(). sys[lat.neighbors()]
= -t then sets all of those hopping matrix elements at once. In order to set
values for all the nth-nearest neighbors at once, one can similarly use
sys[lat.neighbors(n)] = -t. More detailed example of using
HoppingKind directly will be provided in
Matrix structure of on-site and hopping elements.
The left lead is constructed in an analogous way:
lead = kwant.Builder(kwant.TranslationalSymmetry((-a, 0)))
lead[(lat(0, j) for j in xrange(W))] = 4 * t
lead[lat.neighbors()] = -t
The previous example duplicated almost identical code for the left and
the right lead. The only difference was the direction of the translational
symmetry vector. Here, we only construct the left lead, and use the method
reversed of Builder to obtain a copy
of a lead pointing in the opposite direction. Both leads are attached as
before and the finished system returned:
sys.attach_lead(lead)
sys.attach_lead(lead.reversed())
return sys
The remainder of the script has been organized into two functions. One for the plotting of the conductance.
def plot_conductance(sys, energies):
# Compute conductance
data = []
for energy in energies:
smatrix = kwant.smatrix(sys, energy)
data.append(smatrix.transmission(1, 0))
pyplot.figure()
pyplot.plot(energies, data)
pyplot.xlabel("energy [t]")
pyplot.ylabel("conductance [e^2/h]")
pyplot.show()
And one main function.
def main():
sys = make_system()
# Check that the system looks as intended.
kwant.plot(sys)
# Finalize the system.
sys = sys.finalized()
# We should see conductance steps.
plot_conductance(sys, energies=[0.01 * i for i in xrange(100)])
Finally, we use the following standard Python construct [3] to execute
main if the program is used as a script (i.e. executed as
python quantum_wire_revisited.py):
if __name__ == '__main__':
main()
If the example, however, is imported inside Python using import
quantum_wire_revisted as qw, main is not executed automatically.
Instead, you can execute it manually using qw.main(). On the other
hand, you also have access to the other functions, make_system and
plot_conductance, and can thus play with the parameters.
The result of the example should be identical to the previous one.
We have seen different ways to add lattice points to a
Builder. It allows to
For technical reasons it is not possible to add several points using a tuple of sites. Hence it is worth noting a subtle detail in
sys[(lat(x, y) for x in range(L) for y in range(W))] = 4 * t
Note that (lat(x, y) for x in range(L) for y in range(W)) is not
a tuple, but a generator.
Let us elaborate a bit more on this using a simpler example:
>>> a = (0, 1, 2, 3)
>>> b = (i for i in xrange(4))
Here, a is a tuple, whereas b is a generator. One difference is that one can subscript tuples, but not generators:
>>> a[0]
0
>>> b[0]
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: 'generator' object is unsubscriptable
However, both can be used in for-loops, for example.
In the example, we have added all the hoppings using
HoppingKind. In fact,
hoppings can be added in the same fashion as sites, namely specifying
A hopping is defined using two sites. If several hoppings are added at once, these two sites should be encapsulated in a tuple. In particular, one must write:
sys[((lat(0,j+1), lat(0, j)) for j in xrange(W-1)] = ...
or:
sys[[(site1, site2), (site3, site4), ...]] = ...
You might wonder, why it is then possible to write for a single hopping:
sys[site1, site2] = ...
instead of
sys[(site1, site2)] = ...
In fact, due to the way python handles subscripting, sys[site1, site2]
is the same as sys[(site1, site2)].
(This is the deeper reason why several sites cannot be added as a tuple – it would be impossible to distinguish whether one would like to add two separate sites, or one hopping.
Footnotes
| [3] | http://docs.python.org/library/__main__.html |