Quantum transport simulations made easy
Kwant is a free (open source) Python package for numerical calculations on tight-binding models with a strong focus on quantum transport. It is designed to be flexible and easy to use. Thanks to the use of innovative algorithms, Kwant is often faster than other available codes, even those entirely written in the low level FORTRAN and C/C++ languages.
Tight-binding models can describe a vast variety of systems and phenomena in quantum physics. Therefore, Kwant can be used to simulate metals, graphene, topological insulators, quantum Hall effect, superconductivity, spintronics, molecular electronics, any combination of the above, and many other things.
Kwant does not use the traditional input files often found in scientific software packages. Instead, one writes short programs in the powerful yet easy-to-learn Python language. These programs define a system and calculate its quantum properties (conductance, density of states, etc). This workflow can be summarized as follows:
Kwant was designed to be easy to use: Section 2 of the Kwant paper contains a line-by-line walkthrough of a program very similar to the one used to generate the above image. That complete Python script is 26 lines long (including comments).
Examples of Kwant usage
The following examples are meant to give an overview of what is possible with Kwant. The tutorial section of Kwant documentation and the Kwant paper each contain several pedagogical examples with line-by-line explanations (zipfile of all examples).
Graphene flake
The complete code that constructs the graphene flake shown on the right side is
def disk(pos): x, y = pos return x**2 + y**2 < 8**2 lat = kwant.lattice.honeycomb() syst = kwant.Builder() syst[lat.shape(disk, (0, 0))] = 0 syst[lat.neighbors()] = -1
In addition to the flake itself, the image also shows the wave function of a low energy eigenstate. The size of each circle is proportional to the wave function probability amplitude on that site. It can be clearly seen that the wave function is peaked near the zigzag segments of the boundary, as expected for graphene quantum dots.
Taken from the Kwant plotting tutorial.
Quantum Hall effect
One of the most common applications of Kwant is to calculate the conductance of a nanoelectronic system. The plot on the left shows the conductance through a 2-d electron gas as a function of magnetic flux. The quantization of conductance that is visible (plateaus) is the hallmark of the quantum Hall effect. The third plateau does not develop due to a constriction in the system that leads to backscattering. The scattering wave function from the left lead at magnetic field strength corresponding to the middle of the third QHE plateau is shown on the right.
Taken from example 6 of the Kwant paper.
3-d system: Majorana states

Kwant allows systems of any dimensionality, for example three-dimensional ones. This image shows a 3-d model of a semiconducting quantum wire (gray cylinder). The red region is a tunnel barrier, used to measure tunneling conductance, the blue region is a superconducting electrode. In this simulated device, a Majorana bound state appears close to the superconducting-normal interface.
Taken from an unpublished work by S. Mi, A. R. Akhmerov, and M. Wimmer.
Numerical experiment: flying qubit
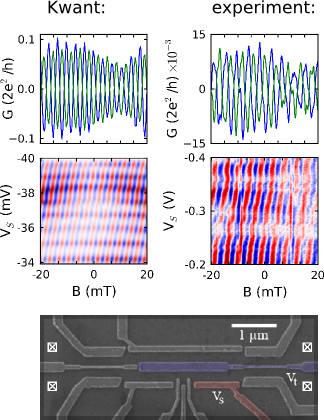
Numerical simulations and experimental results for a flying qubit sample made in a GaAs/GaAlAs heterostrucutre. The Kwant simulations were performed with particular attention to a realistic model of the confining potential seen by the electrons. This allows for rather subtle aspects of the experiment could be reproduced. Such "numerical experiments" can not only be used to interpret the experimental data but also can help to design the sample geometry and in to choose the right materials.
Taken from an unpublished work by T. Bautze et al. See Yamamoto et al., Nature Nanotechnology 7, 247 (2012) for details about the experiment.
Conductance of a Corbino disk in a quantum Hall regime
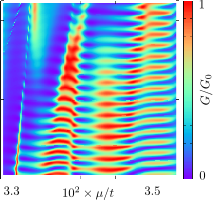
Transport properties of a Corbino disk across a quantum Hall transition. Left: geometry of the sample consisting of a ring-shaped two-dimensional electron gas (grey) in a perpendicular magnetic field. Right: conductance across the transition, showing quantized conductance peaks.
Taken from I. C. Fulga, F. Hassler, A. R. Akhmerov, C. W. J. Beenakker, Phys. Rev. B 84, 245447 (2011); arXiv:1110.4280.